- 1,402
- 1,556
En esta tercera parte de este tutorial, como teníamos planificado, vamos a comenzar a programar el intérprete de ecuaciones matemáticas.
En primer lugar, para lograr esto nos será necesario reconocer los distintos elementos considerados legales de acuerdo a la gramática de una expresión matemática tal cual la definimos más o menos sin llegar a, valga la redundancia, la última expresión; estos elementos identificados dentro de la secuencia de caracteres de un texto fuente, son símbolos formados también por una determinada secuencia de caracteres, conocidos como tokens o lexemas.
En una parte anterior mencionamos como la pieza de software encargada de llevar a cabo el reconocimiento de los lexemas válidos dentro de una cadena de caracteres o texto fuente se denomina analizador lexicográfico.
El analizador sintáctico se sirve del analizador lexicográfico para obtener un lexema detrás de otro, sin necesidad de lidiar con la secuencia de caracteres sin identificar de un programa fuente, garantizando que cada lexema o token obtenido sea válido, y le sirva para realizar su propia tarea de reconocer si la secuencia de lexemas a su vez se considera correcta sintácticamente hablando, todo esto de acuerdo con lo expresado en la misma gramática.
Es decir, el analizador lexicográfico utiliza la gramática para reconocer un token dado a partir de una secuencia de caracteres, porque en dicha gramática está definido cómo está compuesto digamos un identificador, y cuáles caracteres son válidos a la hora de nombrarlo, en tanto el analizador sintáctico le pide al analizador lexicográfico todos los lexemas uno detrás de otro, y usa la gramática para comprobar si la secuencia de los lexemas se puede considerar legal, puesto en dicha gramática todo esto también está expresado.
El componente siguiente de un compilador o un intérprete, como me parece también mencioné, es el analizador semántico, y tal vez no hablé de las rutinas semánticas, o por lo menos usando ese nombre, cuando comenté lo de generar el código. El primero se encarga de comprobar la validez del código escrito en un lenguaje de programación en cuanto a su sentido, y en cuanto a las rutinas, sirven para generar el código objeto cuando se trata de un compilador, o para llevar a cabo lo demandado por cada una de las instrucciones en los intérpretes.
En todo caso, a pesar de existir una teoría detrás de los analizadores lexicográficos y de todos los demás, nosotros no vamos a detenernos en nada de esto, no hablaremos de autómatas finitos deterministas ni de otros mecanismos de reconocimiento, porque no lo necesitamos, y sobre eso existen extensos libros, para nosotros basta saber todo lo antes expuesto.
¿Qué se necesita para hacer un analizador lexicográfico?
En nuestro caso particular nada más necesitaremos un analizador lexicográfico básico, puesto no vamos a analizar toda la gramática de un lenguaje de programación, sino nada más la gramática de una ecuación matemática, sin embargo, todo analizador de esta clase, como se ha dicho, debe de ser capaz de identificar los distintos caracteres considerados válidos en la secuencia de caracteres de entrada, en ocasiones sólo para ignorarlos, como cuando se trata de un espacio en blanco, y en otras con el fin de reunirlos convenientemente hasta reconocer un lexema válido (algunos lexemas están compuestos de un solo símbolo, como los operadores, y otros de muchos, como pasa con las palabras reservadas).
El analizador lexicográfico deberá detenerse y reportar un error si encuentra como parte de la cadena de entrada un símbolo o carácter no válido en la gramática.
Por todo lo dicho, un analizador lexicográfico debe disponer de una serie de funciones o subrutinas básicas, como las nombradas a continuación:
En primer lugar, para lograr esto nos será necesario reconocer los distintos elementos considerados legales de acuerdo a la gramática de una expresión matemática tal cual la definimos más o menos sin llegar a, valga la redundancia, la última expresión; estos elementos identificados dentro de la secuencia de caracteres de un texto fuente, son símbolos formados también por una determinada secuencia de caracteres, conocidos como tokens o lexemas.
En una parte anterior mencionamos como la pieza de software encargada de llevar a cabo el reconocimiento de los lexemas válidos dentro de una cadena de caracteres o texto fuente se denomina analizador lexicográfico.
El analizador sintáctico se sirve del analizador lexicográfico para obtener un lexema detrás de otro, sin necesidad de lidiar con la secuencia de caracteres sin identificar de un programa fuente, garantizando que cada lexema o token obtenido sea válido, y le sirva para realizar su propia tarea de reconocer si la secuencia de lexemas a su vez se considera correcta sintácticamente hablando, todo esto de acuerdo con lo expresado en la misma gramática.
Es decir, el analizador lexicográfico utiliza la gramática para reconocer un token dado a partir de una secuencia de caracteres, porque en dicha gramática está definido cómo está compuesto digamos un identificador, y cuáles caracteres son válidos a la hora de nombrarlo, en tanto el analizador sintáctico le pide al analizador lexicográfico todos los lexemas uno detrás de otro, y usa la gramática para comprobar si la secuencia de los lexemas se puede considerar legal, puesto en dicha gramática todo esto también está expresado.
El componente siguiente de un compilador o un intérprete, como me parece también mencioné, es el analizador semántico, y tal vez no hablé de las rutinas semánticas, o por lo menos usando ese nombre, cuando comenté lo de generar el código. El primero se encarga de comprobar la validez del código escrito en un lenguaje de programación en cuanto a su sentido, y en cuanto a las rutinas, sirven para generar el código objeto cuando se trata de un compilador, o para llevar a cabo lo demandado por cada una de las instrucciones en los intérpretes.
En todo caso, a pesar de existir una teoría detrás de los analizadores lexicográficos y de todos los demás, nosotros no vamos a detenernos en nada de esto, no hablaremos de autómatas finitos deterministas ni de otros mecanismos de reconocimiento, porque no lo necesitamos, y sobre eso existen extensos libros, para nosotros basta saber todo lo antes expuesto.
¿Qué se necesita para hacer un analizador lexicográfico?
En nuestro caso particular nada más necesitaremos un analizador lexicográfico básico, puesto no vamos a analizar toda la gramática de un lenguaje de programación, sino nada más la gramática de una ecuación matemática, sin embargo, todo analizador de esta clase, como se ha dicho, debe de ser capaz de identificar los distintos caracteres considerados válidos en la secuencia de caracteres de entrada, en ocasiones sólo para ignorarlos, como cuando se trata de un espacio en blanco, y en otras con el fin de reunirlos convenientemente hasta reconocer un lexema válido (algunos lexemas están compuestos de un solo símbolo, como los operadores, y otros de muchos, como pasa con las palabras reservadas).
El analizador lexicográfico deberá detenerse y reportar un error si encuentra como parte de la cadena de entrada un símbolo o carácter no válido en la gramática.
Por todo lo dicho, un analizador lexicográfico debe disponer de una serie de funciones o subrutinas básicas, como las nombradas a continuación:
| Nombre de la función o subrutina | Propósito |
| GetCharacter() | Obtener un carácter de la secuencia de caracteres de entrada. |
| IsAlpha%(c As String) | Comprueba “c” y devuelve verdadero si es un carácter alfabético |
| IsDigit%(c As String) | Combrueba “c” y devuelve verdadero si es un dígito de “0” a “9”. |
| IsWhite%(c As String) | Comprueba “c” y devuelve verdadero si es un espacio en blanco. |
| IsAddOp%(c As String) | Comprueba “c” y devuelve verdadero si se trata de un operador “+” o “-” |
| IsMulOp%(c As String) | Comprueba “c” y devuelve verdadero si se trata de un operador “*” o “/” |
| IsParentheses(c As String) | Comprueba “c” y devuelve verdadero si se trata de un símbolo paréntesis “(” o “)” |
El contenido de la tabla mostrada nos enseña como las subrutinas o funciones usadas por el analizador lexicográfico reflejan lo definido en la gramática, aun cuando todavía nos faltarían algunas más, las cuales no listaremos pero si deben ser implementadas de modo dicho analizador pueda reconocer todos los símbolos válidos.
La subrutina GetCharacter podría implementarse como sigue:
La subrutina GetCharacter podría implementarse como sigue:
Código:
Sub GetCharacter()
If Position < Len(Expression) Then
Position = Position + 1
Character = UCase$(Mid$(Expression, Position, 1))
End If
End SubEn esta subrutina hacemos uso de una variable global Integer de nombre Position, en la cual se guarda, como su nombre lo indica, la posición del carácter a ser leído dentro de la cadena de caracteres de entrada. La cadena de entrada o ecuación matemática estará guardada a su vez en la variable global String de nombre Expression. Por fin, el carácter es leído por medio de la función Mid del BASIC y es guardado en una variable global String de nombre Character de donde será tomado cuando nos veamos en la necesidad de hacerlo.
Nota: La función de BASIC denominada UCase convierte una cadena en mayúsculas, con lo cual el carácter guardado en Character estará en mayúsculas en caso de ser un carácter alfabético, y por tanto no distinguiremos entre mayúsculas y minúsculas en las ecuaciones a ser interpretadas (la variable Volumen será igual a VOLUMEN o a volumen).
Por su parte, las funciones listadas son casi iguales entre ellas, salvo por reconocer el elemento indicado por su nombre (Letra, Dígito, Espacio en blanco, etc.).
Las líneas de código siguientes muestran como sería la función IsAlpha destinada a reconocer una letra o carácter alfabético:
Nota: La función de BASIC denominada UCase convierte una cadena en mayúsculas, con lo cual el carácter guardado en Character estará en mayúsculas en caso de ser un carácter alfabético, y por tanto no distinguiremos entre mayúsculas y minúsculas en las ecuaciones a ser interpretadas (la variable Volumen será igual a VOLUMEN o a volumen).
Por su parte, las funciones listadas son casi iguales entre ellas, salvo por reconocer el elemento indicado por su nombre (Letra, Dígito, Espacio en blanco, etc.).
Las líneas de código siguientes muestran como sería la función IsAlpha destinada a reconocer una letra o carácter alfabético:
Código:
Function IsAlpha%(c As String)
IsAlpha = (Asc(c) >= 65) And (Asc(c) <= 90)
End FunctionEn este caso usamos la función BASIC Asc para obtener el código ASCII del elemento en la variable “c”, y comparamos ese código para ver si se trata de una letra de la “A” a la “Z” (los códigos ASCII del rango de letras de la “A” a la “Z” se corresponden con los números de 65 a 90).
En general como se ha mencionado necesitaremos funciones básicas como estas de modo podamos detectar todos los distintos símbolos legales en la secuencia.
Es decir, debe ser evidente la necesidad de una función para reconocer un “.” puesto un número real lo posee, tal como lo expresa la gramática de un número, aun cuando es cierto esta no fue expuesta en su momento en ese detalle y nos limitamos a esto:
En general como se ha mencionado necesitaremos funciones básicas como estas de modo podamos detectar todos los distintos símbolos legales en la secuencia.
Es decir, debe ser evidente la necesidad de una función para reconocer un “.” puesto un número real lo posee, tal como lo expresa la gramática de un número, aun cuando es cierto esta no fue expuesta en su momento en ese detalle y nos limitamos a esto:
<number> ::= [<digit>]+
En este momento podríamos cambiar la definición anterior para hacerla un poco más abarcadora de manera se comprenda la idea:
<number> ::= <integer> | <integer> '.' <integer>
<integer> ::= [<digit>]+
<digit> ::= '0' | '1' | '2' | '3' | '4' | '5' | '6' | '7' | '8' | '9'
<integer> ::= [<digit>]+
<digit> ::= '0' | '1' | '2' | '3' | '4' | '5' | '6' | '7' | '8' | '9'
Pero como se pueden dar cuenta, esta versión un poco más extendida de <number>, a pesar de mostrarnos como es necesario reconocer un “.” por representar un número con punto decimal, todavía resulta insuficiente para los números en notación científica.
En resumen, la intención de esto es mostrarles sin lugar a dudas cómo el analizador lexicográfico se basa en los símbolos o caracteres válidos definidos en la gramática de una expresión matemática y depende de ella.
Las funciones mencionadas nos van a servir como base para hacer otras funciones o subrutinas de reconocimiento de orden superior como comentamos seguidamente.
La subrutina SkipWhite puede servirnos de demostración:
En resumen, la intención de esto es mostrarles sin lugar a dudas cómo el analizador lexicográfico se basa en los símbolos o caracteres válidos definidos en la gramática de una expresión matemática y depende de ella.
Las funciones mencionadas nos van a servir como base para hacer otras funciones o subrutinas de reconocimiento de orden superior como comentamos seguidamente.
La subrutina SkipWhite puede servirnos de demostración:
Código:
Sub SkipWhite()
While IsWhite(Character)
GetCharacter
Wend
End SubLa subrutina SkipWhite, como su nombre lo indica bastante bien, será utilizada por el analizador lexicográfico para saltarse todos los espacios en blanco en la secuencia de entrada, puesto estos no tienen significado para el analizador sintáctico.
Nota: En un analizador lexicográfico de un lenguaje de programación donde el código se escribe en muchas líneas, SkipWhite también se saltaría los retornos del carro y los caracteres de nueva línea.
Pero vamos a dar un salto y ver la función principal del analizador lexicográfico, la cual se pudiera llamar GetToken, porque de todos modos en este instante debería haberse entendido la idea, conociendo la función del analizador lexicográfico de reconocer e ir entregando todos los lexemas válidos también conocidos como tokens según estos son descritos por la gramática:
Nota: En un analizador lexicográfico de un lenguaje de programación donde el código se escribe en muchas líneas, SkipWhite también se saltaría los retornos del carro y los caracteres de nueva línea.
Pero vamos a dar un salto y ver la función principal del analizador lexicográfico, la cual se pudiera llamar GetToken, porque de todos modos en este instante debería haberse entendido la idea, conociendo la función del analizador lexicográfico de reconocer e ir entregando todos los lexemas válidos también conocidos como tokens según estos son descritos por la gramática:
Código:
Function GetToken$()
SkipWhite
If IsAlpha(Character) Then
GetToken = GetIdentifier
ElseIf IsDigit(Character) Then
GetToken = GetNumber
ElseIf IsOperator(Character) Or IsParenthesis(Character) Or IsComma(Character) Or IsTerminator(Character) Then
GetToken = Character
GetCharacter
Else
Error 255
End If
End FunctionLa función GetToken debería devolver un lexema con cada llamada a ella, o emitir un error en caso de encontrarse con un carácter no válido como parte de la secuencia de entrada; se trata de una función bastante simplificada, puesto probablemente no sea usada más adelante, para lograr una mejor integración entre el analizador lexicográfico y el analizador sintáctico.
En ella hacemos uso de otras funciones como las mencionadas de reconocimiento de distintos símbolos o caracteres, y de otras como GetIdentifier, destinada a obtener un identificador (nombre de variable o función), o GetNumber, destinada a reconocer un número.
Las funciones GetIdentifier y GetNumber, como sucede con algunas de las otras, no serán listadas en este texto, no obstante, cada cual podrá verlas si descarga el fuente del programa donde están implementadas.
En particular, la función GetNumber debería ser capaz de reconocer un número entero o un número real, así como un número en notación científica expresado como se lo suele hacer en los sistemas informáticos (como en 1.36e-14)
El código a continuación nos puede servir para probar lo hecho hasta ahora:
En ella hacemos uso de otras funciones como las mencionadas de reconocimiento de distintos símbolos o caracteres, y de otras como GetIdentifier, destinada a obtener un identificador (nombre de variable o función), o GetNumber, destinada a reconocer un número.
Las funciones GetIdentifier y GetNumber, como sucede con algunas de las otras, no serán listadas en este texto, no obstante, cada cual podrá verlas si descarga el fuente del programa donde están implementadas.
En particular, la función GetNumber debería ser capaz de reconocer un número entero o un número real, así como un número en notación científica expresado como se lo suele hacer en los sistemas informáticos (como en 1.36e-14)
El código a continuación nos puede servir para probar lo hecho hasta ahora:
Código:
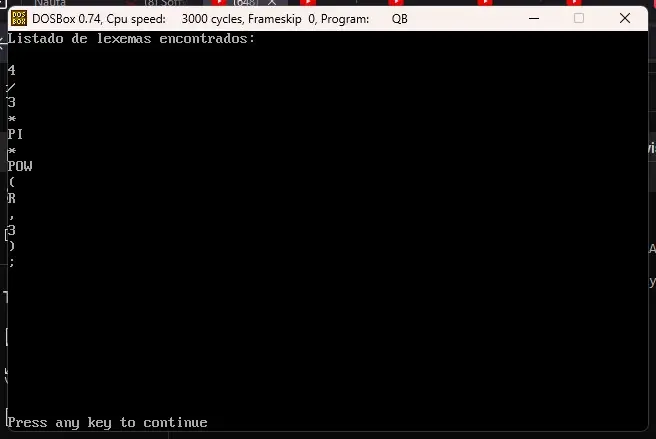
Position = 0
Expression = “4/3*Pi*Pow(r,3);”
GetCharacter
While Position < Len(Expression)
Print GetToken
Wend
Print GetTokenLa corrida del programa con la expresión matemática indicada debería dar como resultado la salida presentada en la imagen:
Los interesados en verlo pueden descargar el fuente del programa en este enlace: Lex.zip
En todo caso, como deben de saber, se trata nada más del analizador lexicográfico del intérprete de ecuaciones, en una próxima parte comenzaremos con la implementación del analizador sintáctico y de lo restante.
Nota: El código del programa no ha utilizado códigos de error diferenciados dado esto se está haciendo sólo con fines educativos, todos los errores lanzados desde dentro de las distintas subrutinas y funciones tienen un código común número 255.
En todo caso, como deben de saber, se trata nada más del analizador lexicográfico del intérprete de ecuaciones, en una próxima parte comenzaremos con la implementación del analizador sintáctico y de lo restante.
Nota: El código del programa no ha utilizado códigos de error diferenciados dado esto se está haciendo sólo con fines educativos, todos los errores lanzados desde dentro de las distintas subrutinas y funciones tienen un código común número 255.