Articulo Haciendo un intérprete de ecuaciones matemáticas: Cuarta parte (final)

pcarballosa · 23 Enero 2024

En la tercera parte del tutorial, terminamos haciendo un analizador lexicográfico de lo más básico (y eso si podemos llamarle así puesto nada más devolvía los lexemas sin ninguna otra información sobre ellos), y en esta continuaremos desarrollando otras partes del intérprete de ecuaciones matemáticas, entre ellas el analizador sintáctico, hasta terminarlo.

En realidad, como esto se trata de ir interpretando (como su nombre lo indica) una ecuación pasada en forma de una cadena de texto, dicho analizador sintáctico estará bastante integrado con las rutinas del analizador lexicográfico antes vistas, y también con las encargadas de obtener los resultados.

Por otro lado, también para facilitar esa integración, se realizarán modificaciones en funciones como GetNumber, para devolver un valor numérico en vez de un texto con el lexema correspondiente como se hacía.

Pero no nos detendremos en listar esos cambios en este texto, para ahorrar espacio y tiempo, porque son básicos y podrán ser vistos si se descargan el código fuente en la parte final, nada más los comento porque así estarán avisados.

En adición, a nuestro analizador lexicográfico también le faltaron unas pocas funciones más, innecesarias cuando lo hicimos, pero imprescindibles ahora para cumplir con los objetivos.

En efecto, como he mencionado, el analizador lexicográfico no nos daba toda la información, sólo los nombres o símbolos de los lexemas, y ahora no nos basta con obtener el lexema de un identificador, necesitamos distinguir si se trata de una función o de una variable (los únicos identificadores usados en el intérprete), para esto se han creado las funciones:

Nombre de la función	Propósito
IsFunction% (Token As String)	Comprueba si Token es una función reconocida y devuelve verdadero de ser así.
IsVariable%(Token As String)	Comprueba si Token es una variable reconocida y devuelve verdadero de ser así.

Las funciones IsFunction e IsVariable hacen su trabajo buscando en las respectivas tablas para comprobar si el nombre contenido en Token concuerda con el nombre de una función registrada o de una variable previamente declarada, por tanto, también deberán ser creadas las mencionadas tablas (arreglos) de funciones y variables, así como una subrutina para registrar en la tabla de las variables los nombres de las nuevas variables creadas y una función para obtener su valor actual a partir de su nombre.

Nota: En un sistema funcional se necesitaría también una subrutina para liberar una variable una vez no se necesite (tener disponible la posición del arreglo para usarla en otra variable).

En resumen, todo eso lo podrán ver si revisan el código fuente, y como he dicho, son piezas relativamente sencillas del intérprete de ecuaciones.

En este momento vamos a proceder con la implementación del analizador sintáctico (y las otras partes necesarias para ponerlo a funcionar), y vamos a ver cómo, tal como pasó cuando se hizo el analizador lexicográfico, su estructura es un reflejo más o menos exacto de la gramática de los elementos de una expresión matemática.

La gramática indica como una expresión matemática se expresa como:

<expression> ::= <unary op> <term> [<addop> <term>]*

Por tanto, vamos a necesitar una funcion GetExpression donde se recree lo expresado por la notación listada (como esto es un intérprete esta función intentará calcular una expresión y devolver un resultado).

Pero como podemos ver, una expresión está compuesta por términos, y por tanto para validar una expresión y calcular su resultado, deberemos reconocer la validez de los términos por los cuales está compuesta.

La gramática nos dice un término se expresa como:

<term> ::= <factor> [<mulop> <factor>]*

En este caso la función podemos llamarla GetTerm y calculará el valor de un término si lo reconoce como válido, no obstante, como un término a su vez está compuesto por uno o más factores, una vez más nos vemos en la necesidad de una función capaz de analizar estos factores.

El factor se expresa como sigue según la gramática:

El factor por tanto parece ser el último nivel, y más complicado, y podemos empezar por implementar esa función, dado de todos modos todas se relacionan unas con otras por ser una expresión un ente recursivo.

La gramática nos muestra como un factor puede ser un número (<number>), una expresión (<expression>) entre paréntesis, o una variable (<variable>), para el primero y el último de los cuales tenemos funciones creadas desde cuando se implementó el analizador lexicográfico limitado.

Además, en la notación de la gramática de factor antes mostrada nos faltaba tener en cuenta las funciones, y ahora debemos recordarlo, así como también deberemos tener presente otros detalles como el operador de asignación, etc., a pesar de no haberlos representado en la gramática.

La gramática de una función podría ser como esta:

En la notación anterior podemos ver una relación recursiva nuevamente.

La función GetFactor está listada a continuación:

Código:

Function GetFactor#
  Dim Token As String
  Dim Parameter1 As Double
  Dim Parameter2 As Double
  Dim Result As Double
  SkipWhite
  If IsDigit(Character) Then
    Result = GetNumber
  ElseIf Character = "(" Then
    Match "("
    Result = GetExpression
    Match ")"
  ElseIf IsAlpha(Character) Then
    Token = GetIdentifier
    If IsFunction(Token) Then
      Match "("
      Select Case Token
        Case "SQRT"
          Result = SQR(GetExpression)
        Case "SQR"
          Result = GetExpression ^ 2
        Case "POW"
          Parameter1 = GetExpression
          Match ","
          Parameter2 = GetExpression
          Result = Exp(Parameter2 * Log(Parameter1))
        Case Else
          ‘Función no definida en la tabla de funciones
          Error 255
      End Select
      Match ")"
    ElseIf IsVariable(Token) Then
        Result = GetVariable(Token)
        If Character = "=" Then
          Match "="
          Result = GetExpression
          SetVariable Token, Result
        End If
    ElseIf IsAddOp(Character) Then
      Result = GetExpresion
    Else
      'Número, expresión, o identificador (función o variable) esperados
      Error 255
    End If
  End If
  GetFactor = Result
End Function

El listado de código anterior muestra una evidente correspondencia con lo expresado en la gramática de los factores.

La subrutina Match es la encargada de comprobar si la sintaxis es correcta, y reportar un error si no se encuentra lo esperado según lo revela la gramática, esta subrutina se podría llamar Check por su función.

La función GetTerm también es un reflejo de la gramática de un término:

Código:

Function GetTerm#
  Dim Result As Double
  Result = GetFactor
  While IsMulOp(Character)
    Select Case Character
      Case "*"
        Match "*"
        Result = Result * GetFactor
      Case "/"
        Match "/"
        Result = Result / GetFactor
    End Select
  Wend
  GetTerm = Result
End Function

Por último, el mismo caso se da con la función GetExpression, como era de esperarse, una vez más un reflejo de la gramática de una expresión:

Código:

Function GetExpression#
  Dim Result As Double
  If IsAddOp(Character) Then
    Position = Position - 1
    Character = "0"
  End If
  Result = GetTerm
  While IsAddOp(Character)
    Select Case Character
      Case "+"
        Match "+"
        Result = Result + GetTerm
      Case "-"
        Match "-"
        Result = Result – GetTerm
    End Select
  Wend
  GetExpression = Result
End Function

El resto de las subrutinas o funciones no las describo porque son mucho más simples y resulta irrelevante.

Por fin, el programa principal listado a continuación evalúa una función definida en la variable String de nombre Expression:

Código:

Cls

Print "Calcular volumen de la esfera de radio 10:"
Print

Expression = "Vol=4/3*Pi*Pow(r,3);" 'Cambiar ecuación para hacer pruebas

Print "Expresión matemática: ";
Print Expression
Print

On Error Goto ErrorHandler

SetVariable "Vol", 0
SetVariable "Pi", 3.14159
SetVariable "r", 10

SolverExpression

Print "El resultado del volumen de la esfera obtenido para los valores establecidos es: ";
Print GetVariable("Vol")

End

ErrorHandler:
  If Err = 255 Then
    Print "Error detectado durante el procesamiento del símbolo cerca de: " + Str$(Position)
    Print "El programa será terminado"
  End If

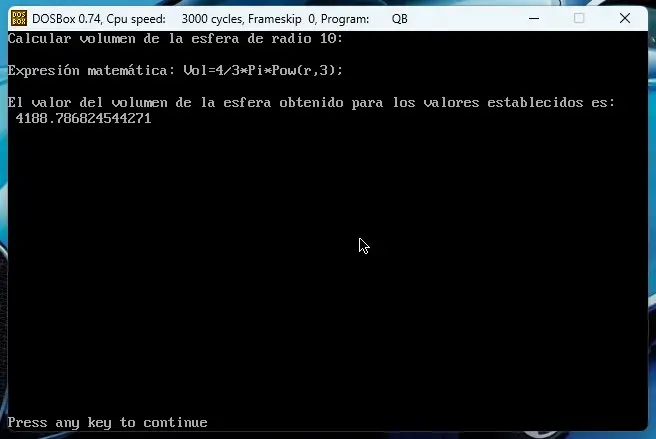
End

El resultado de correr este programa pueden verlo en la imagen:

En resumen, con esto disponemos de un intérprete de ecuaciones matemáticas hecho en lenguaje BASIC, y podemos utilizarlo para crear una calculadora capaz de resolver ecuaciones numéricamente.

Por supuesto, todavía sería necesario testearlo, y agregar más código para comprobar un par de cosas pasadas por alto, pero en general funciona y debería poder resolver la o las ecuaciones pasadas como entrada en forma de una cadena de caracteres.

Nota: En la tabla de funciones del intérprete nada más se definieron tres de ellas para simplificar la tarea, sin embargo, nada impide agregarle más funciones, recordando se debe colocar el código correspondiente para comprobar la sintaxis y obtener un resultado en la función GetFactor.

El código fuente del programa puede ser descargado desde este enlace: ExpInp.zip

¡Bienvenido!

Articulo Haciendo un intérprete de ecuaciones matemáticas: Cuarta parte (final)

pcarballosa